MCTS란?

Monte Carlo Tree Search(MCTS)는 2006년 Rémi Coulom이란 사람이 Monte Carlo Method를 게임 tree search에 접목하면서 만든 용어이다. 여기서 Monte Carlo는 확률적인 문제에 모나코의 유명한 도박장 이름(Monte Carlo)을 따서 붙이는 관습에서 온 것으로 보인다. 쉽게 말해 확률적 Tree Search라고 보아도 무방하지 않을까?

Monte Carlo Method는 Random sampling을 반복하여 deterministic(결정론적 문제)한 문제를 해결하는 방법이다. 즉, 특정한 규칙을 따르지만 수학적/알고리즘적으로 분석하여 구현하기에는 너무나도 복잡한 시스템에 대해, 여러번 맨땅에 헤딩하면서 대략적인 규칙을 찾아내어가는 방법이라고 할 수 있겠다. 경제학자들이 경제를 분석할 때, 개개인의 소비에 대해서 분석하지 않고 전체적인 수입/수출액 및 세수 등의 지표로 경기를 분석하는 것과 비슷하다고 생각하면 될 것 같다. MCM은 그 특성상 AI에 접목시키기 너무나도 좋아 보인다.

Monte Carlo Method 예시

 

MCTS는 2012년부터 각광받기 시작했지만, 본격적으로 뜨기 시작한 건 2016년 MCTS 머신러닝을 접목시킨 알파고의 등장 때부터였던 것 같다. 알파고에서 NN이 쓰인 용도는 policy(move selection)랑 value(reward?) 계산이다.

 

MCTS에 대해 설명하기에 앞서, 먼저 알아두면 이해를 도울 몇가지 포인트가 있다.

1. MCTS는 머신러닝 기법이 아닌, 통계적 알고리즘이다. MCTS의 "학습"은 각 노드에서 다음 노드를 선택할 때마다 이루어지며, 기존  대국 족보와 같은 데이터를 사용할 방법은 없다. Markov Process를 가정하므로 오직 현재 상태와 미래 상태만 생각한다.
2. MCTS는 항상 "가장 밸류가 높을 것 같은 노드"를 먼저 탐색한다. 밑에 설명할 비대칭성은 여기서 나오는 것으로, Root로부터 몇번째 레벨인지 상관 없이 Q-value 및 탐색상수만을 사용하여 다음 state를 선택한다.

 

MCTS의 원리

MCTS의 가장 원초적인 설명은 Markov Decision Process(MDP)를 Tree형식으로 나타내고(Expectimax Tree), 해당 트리를 탐색하여 최적, 혹은 주어진 자원 내에서 최선의 결과를 도출하는 알고리즘이다.

MDP는 순차적 의사결정(sequential decision-making) 프레임워크이다. MDP는 stochastic(확률 분포가 있는) non-deterministic(입력값 A에 대해서 항상 B가 나오는 것이 아니라, 확률적으로 B, C, 또는 D가 나올 수 있는) system을 가정한다. 예시로, 주사위를 굴리면 1, 2, 3, 4, 5, 6이 모두 동일한 확률로 나오는데, 이는 uniform distribution을 가진 stochastic nondeterministic 시스템이라고 할 수 있다.

또한, Markov Process는 미래의 상태를 예측하는데 있어 오로지 현재의 데이터만을 사용한다. 과거에 무엇을 했는지에 대한 데이터를 사용한다면, 그것은 Markov Process의 기준을 충족하지 못한다. 더 자세한 설명은 추후 필자가 이에 대해 더 공부하고 나서 작성하도록 하겠다.

 

MCTS의 특징은 다음과 같다:

1. Q-value(특정 action을 선택했을 때의 value)는 random simulation을 통해 도출(MCM)
2. Anytime 알고리즘 (시작 후 언제든지 멈출 수 있고, 멈췄을 때 지금까지 찾은 결과 중 최선의 결과 도출)
3. Asymmetric search (기존 시뮬레이션 결과에 기반하여 트리 탐색, BFS처럼 균일하게 모든 결과 탐색 X)
4. Approximation (전체 결과를 탐색하지는 않고, 큰 search space에서 최적의 결과를 탐색 - 전체 결과 탐색이 가능하다면 MCTS 말고 value iteration과 같은 dynamic programming 기법을 사용하는 것이 나을 것)

반응형

 

MCTS 알고리즘은 다음과 같다.

1. Selection - terminate 되지 않은 노드를 하나 고른다  

   

   Selection stage에서 탐색이 끝나지 않은 노드를 고른다

2. Expansion - 1에서 고른 노드를, 가능한 action 중 하나를 골라 탐색한다

   

   Expansion stage에서 가능한 action 중 하나를 고른다

3. Simulation - 2에서 탐색하기로 결정한 action을 도입 후, terminal state 또는 stopping condition이 나올 때까지 무작위로 가능한 action을 선택한다(random playout). 이론상, 무작위로 선택을 여러번 할 경우 "unbiased estimation"이 도출된다.

   

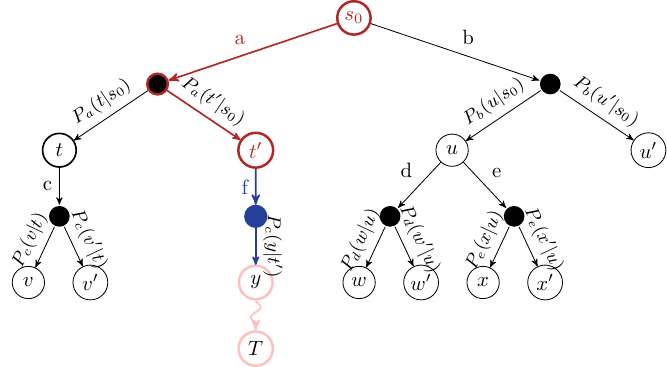
   Simulation stage에서 playout을 통해 terminal stage/stopping condition까지 무작위 action을 취한다

4. Backpropagation - 3에서 얻은 reward(r)을 통해 2-3의 path의 각 state에 대해 Value(V)를 계산한다.

   

   Backpropagation stage에서 초록색 state/action에 대해 Q-value를 업데이트한

    

MCTS에서는 각 Node가 자녀 노드들, 부모 노드 및 action에 대한 pointer, 그리고 해당 노드의 visit 횟수를 저장한다. 

바닐라 MCTS에서는 Selection에 multi-armed bandit 알고리즘을 도입, Q-function을 통해 다음 node를 선정하고, Simulation 때는 random playout때 생성한 노드를 termination까지 간 후에 삭제한다. 

아무래도 Simulation 단계가 domain-specific implementation을 통해 가장 크게 이득을 취할 수 있는 단계일 것으로 생각된다. 자주 사용되는 방법은 heuristic을 사용하여 랜덤 시뮬레이션을 조금 더 자주 나오는 결과로 유도하는 것이라고 한다. 이 단계가 실제 use case에 MCTS를 사용할 때 가장 많이 생각해야 하는 단계일 것이다.

추가로, reward(Q-value)를 계산하는 것 또한 매우 중요하면서도 implementation에 따라 크게 달라질 것이라고 생각되는데, Q-learning이나 SARSA 등을 통해 Q-value의 근사값을 유추하는 방법 또한 많이 쓰인다고 한다. AlphaGo와 그 후계자 AlphaZero는 딥러닝을 통해 Q-value를 유추한다.

 

 

 

Upper Confidence Tree(UCT)

MCTS의 1단계인 Selection stage에서는 multi-armed bandit algorithm이 사용되는데, 이 중 UCB1 알고리즘을 변형하여 사용하는 것이 효과적이여서 개별 카테고리로 분류될 정도로 많이 사용된다고 한다. 즉, UCT = MCTS + UCB1이다.

UCT는 selection에서 다음 알고리즘을 사용한다:

1항: 현재 state(s)에서 가능한 action(a)에 대한 reward (Q(s, a))2항: N(s)는 현재 state가 visit된 횟수, N(s, a)는 현 노드에서 a가 선택된 횟수, Cp는 탐험상수

위 알고리즘은, 현 state(s)에서 가능한 모든 action(A(s)) 중, 특정 a에 대해 1항+2항의 값의 최대값을 주는 a를 선택하는 것이다. 1항은 기본 MCTS에서 사용하는 값이고, 2항은 현 노드에서 특정 a를 반복하는 것을 discourage 하는 것, 즉 다양한 선택을 장려하는 것이라고 보면 될 것 같다. 

 

다음 포스트에서는 바닐라 MCTS를 통해 간단한 게임인 Tic-Tac-Toe와, 게임 보드를 3x3에서 NxN으로 늘렸을 때 MCTS를 도입해 보도록 하겠다. 그 다음에는 AlphaGo 및 AlphaZero에서 사용된 딥러닝 테크닉을 구현하는 것을 목표로 한다.

 

 

참고할만한 자료:

https://en.wikipedia.org/wiki/Monte_Carlo_tree_search

Monte Carlo tree search - Wikipedia

https://medium.com/@_michelangelo_/monte-carlo-tree-search-mcts-algorithm-for-dummies-74b2bae53bfa

Monte Carlo Tree Search (MCTS) algorithm for dummies!

https://gibberblot.github.io/rl-notes/single-agent/mcts.html

Monte-Carlo Tree Search (MCTS) — Mastering Reinforcement Learning

https://arxiv.org/pdf/2103.04931

<2012년 이후 MCTS에 대한 Survey. 2022 작성>